Binder

Phase-dependent SIR models

SIR-derived ODE models (SIR, SIR-D, SIR-F) assume that ODE parameter values are always constant. Can we apply this assumption to real data?

Kaggle: COVID-19 data with SIR model concluded this was No - ODE parameter values change with phases - because measures taken by people changed the situation of COVID-19 outbreak actually. Term “phase” means a sequential dates in which the parameters of SIR-derived models are constant. To remove fluctuations from analysis, “time-dependent” should be avoided.

The first section will show the dynamics of phase-dependent SIR models with sample data.

The Kaggle notebook also suggested detailed steps of applying phase-dependent SIR models to actual data. The second section demonstrates how to divide actual time-series data to phases (time-series segmentation with “S-R change point analysis”). The third section is to estimate ODE parameter values of phases (“ODE parameter estimation”).

With fourth section, we will perform them with actual data of Tokyo/Japan as an example.

[1]:

from copy import deepcopy
from pprint import pprint
import covsirphy as cs
import sympy
cs.__version__

[1]:

'3.1.2'

1. Dynamics of phase-dependent SIR models

Using Dynamics class, we will simulate phase-dependent SIR model with sample data (two phase) as an example.

The 0th phase: 01Jan2022 - 28Feb2022, rho=0.2, sigma=0.075 (preset)
The 1st phase: 01Mar2022 - 30Jun2022, rho=0.4, sigma=0.075

tau value: 1440 [min] (default)

1-1. Define the 0th phase

As the first step, define the 0th (initial) phase with preset ODE parameter values.

[2]:

dyn = cs.Dynamics.from_sample(cs.SIRModel, date_range=("01Jan2022", "30Jun2022"), tau=1440)
# Show summary
dyn.summary()

[2]:
Start End Rt rho sigma 1/beta [day] 1/gamma [day]
Phase
0th 2022-01-01 2022-06-30 2.67 0.2 0.075 5 13

1-2. Define the 1st phase

Get the current settings of initial values of variables and ODE parameter values as a pandas.DataFrame. Then, edit it and register it to the instance.

[3]:

before_df = dyn.register()
before_df

[3]:
Susceptible Infected Recovered Fatal rho sigma
Date
2022-01-01 999000.0 1000.0 0.0 0.0 0.2 0.075
2022-01-02 <NA> <NA> <NA> <NA> <NA> <NA>
2022-01-03 <NA> <NA> <NA> <NA> <NA> <NA>
2022-01-04 <NA> <NA> <NA> <NA> <NA> <NA>
2022-01-05 <NA> <NA> <NA> <NA> <NA> <NA>
... ... ... ... ... ... ...
2022-06-26 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-27 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-28 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-29 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-30 <NA> <NA> <NA> <NA> <NA> <NA>

181 rows × 6 columns

Without NAs:

[4]:

before_df.dropna(how="all")

[4]:
Susceptible Infected Recovered Fatal rho sigma
Date
2022-01-01 999000.0 1000.0 0.0 0.0 0.2 0.075

Edit the dataframe to set the ODE parameter values of the 1st phase.

[5]:

setting_df = dyn.register()
setting_df.loc["01Mar2022", ["rho", "sigma"]] = [0.4, 0.075]
setting_df

[5]:
Susceptible Infected Recovered Fatal rho sigma
Date
2022-01-01 999000.0 1000.0 0.0 0.0 0.2 0.075
2022-01-02 <NA> <NA> <NA> <NA> <NA> <NA>
2022-01-03 <NA> <NA> <NA> <NA> <NA> <NA>
2022-01-04 <NA> <NA> <NA> <NA> <NA> <NA>
2022-01-05 <NA> <NA> <NA> <NA> <NA> <NA>
... ... ... ... ... ... ...
2022-06-26 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-27 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-28 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-29 <NA> <NA> <NA> <NA> <NA> <NA>
2022-06-30 <NA> <NA> <NA> <NA> <NA> <NA>

181 rows × 6 columns

Without NAs:

[6]:

setting_df.dropna(how="all")

[6]:
Susceptible Infected Recovered Fatal rho sigma
Date
2022-01-01 999000.0 1000.0 0.0 0.0 0.2 0.075
2022-03-01 <NA> <NA> <NA> <NA> 0.4 0.075

Register the new settings. Because initial values on 01Mar2022 will be calculated with analytical solution of the 0th phase, they were not registered manually.

[7]:

dyn.register(setting_df)
# Show summary
dyn.summary()

[7]:
Start End Rt rho sigma 1/beta [day] 1/gamma [day]
Phase
0th 2022-01-01 2022-02-28 2.67 0.2 0.075 5 13
1st 2022-03-01 2022-06-30 5.33 0.4 0.075 2 13

High-lightened:

[8]:

dyn.summary().style.highlight_max(subset=["Rt", "rho", "1/beta [day]"])

[8]:
  Start End Rt rho sigma 1/beta [day] 1/gamma [day]
Phase              
0th 2022-01-01 00:00:00 2022-02-28 00:00:00 2.670000 0.200000 0.075000 5 13
1st 2022-03-01 00:00:00 2022-06-30 00:00:00 5.330000 0.400000 0.075000 2 13

With the same way, we can set additional phases, if necessary for your analysis.

1-3. Track ODE parameter values

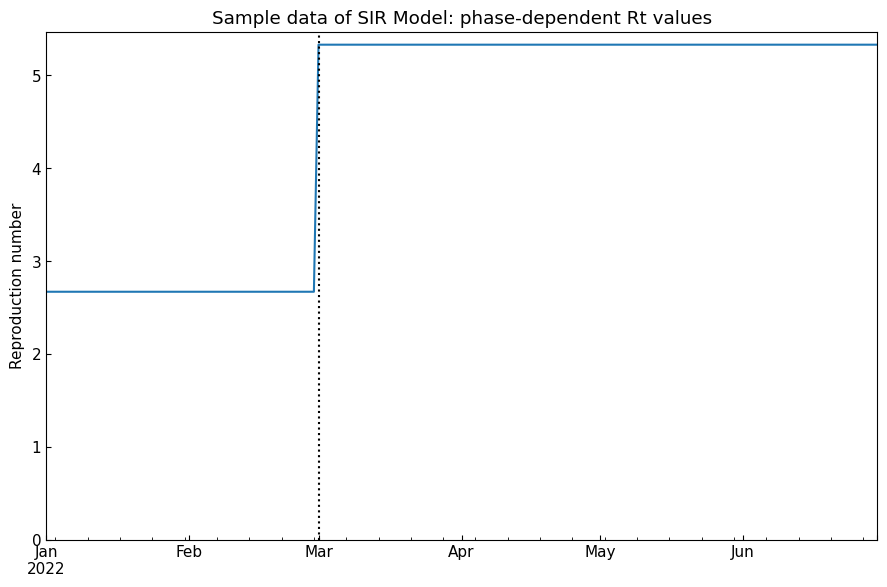
Confirm the phase-dependent ODE parameter values and Rt (reproduction number) by plotting.

[9]:

df = dyn.track()
cs.line_plot(
    df["Rt"],
    title=f"Sample data of {dyn.model_name}: phase-dependent Rt values",
    ylabel="Reproduction number",
    show_legend=False,
    v=dyn.start_dates()[1:]
)
df.loc["27Feb2022": "02Mar2022"].style.highlight_max(subset=["Rt", "rho", "1/beta [day]"])
_images/04_phase_dependent_20_0.png 
[9]:
  Rt rho sigma 1/beta [day] 1/gamma [day]
Date          
2022-02-27 00:00:00 2.670000 0.200000 0.075000 5 13
2022-02-28 00:00:00 2.670000 0.200000 0.075000 5 13
2022-03-01 00:00:00 5.330000 0.400000 0.075000 2 13
2022-03-02 00:00:00 5.330000 0.400000 0.075000 2 13

1-4. Simulation

With Dynamics().simulate(), simulate the phase-dependent ODE model with numerical analysis of each phase. Because we did not specify the initial values on the start date of the 1st phase, simulated values on the 1st phase’s start date will be used as the initial values of the 1st phase.

[10]:

df = dyn.simulate(model_specific=True)
cs.line_plot(df, title=f"Two-phase {dyn.model_name}", v=dyn.start_dates()[1:])
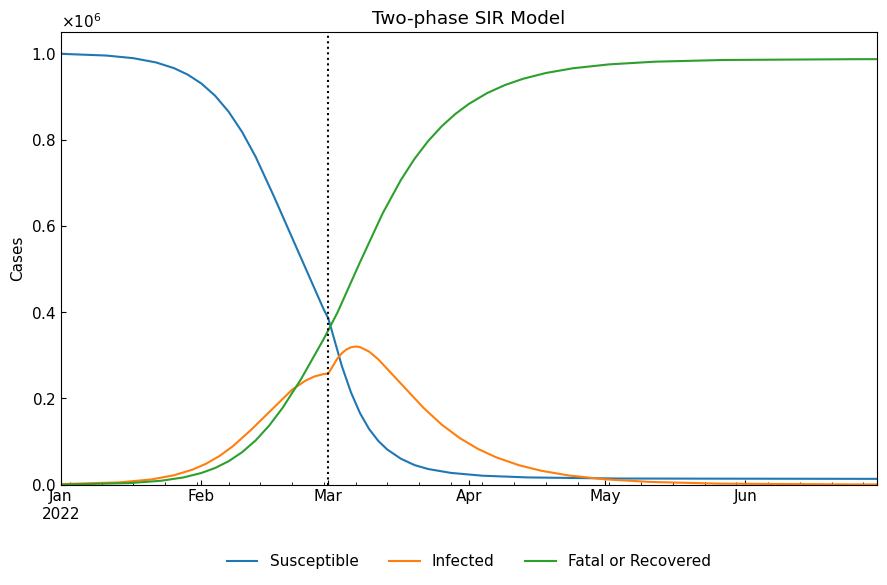
_images/04_phase_dependent_22_0.png

When we need convert model-specific variables to model-free variables (Susceptible/Infected/Fatal/Recovered), we will set model_specific=False (default). SIR model cannot separate “Fatal” cases and “Recovered” cases into different groups. Please use SIR-D model or SIR-F model if the following role is not acceptable for your analysis.

  • “Fatal” is always equal to 0

  • “Recovered” is equal to “Fatal or Recovered” of SIR model

[11]:

df = dyn.simulate(model_specific=False)
cs.line_plot(df, title=f"Two-phase {dyn.model_name}", v=dyn.start_dates()[1:])
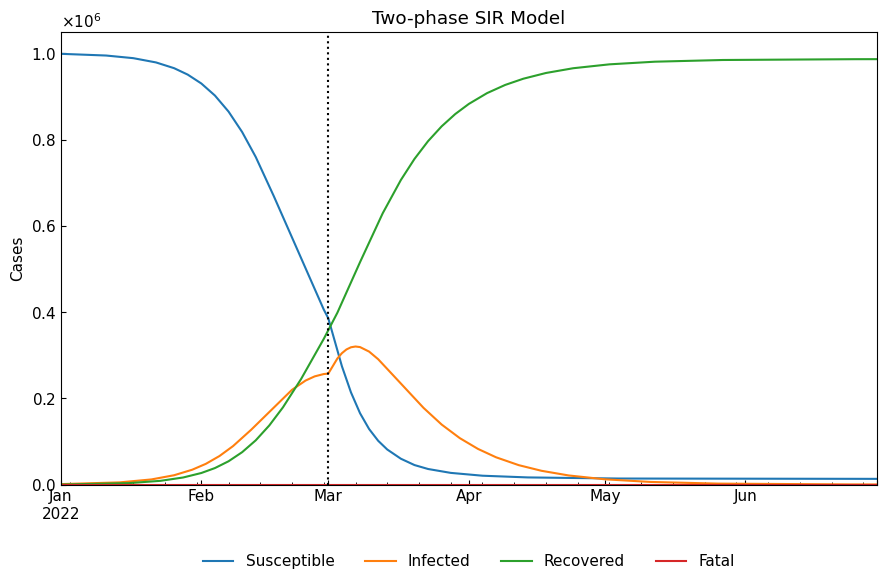
_images/04_phase_dependent_24_0.png

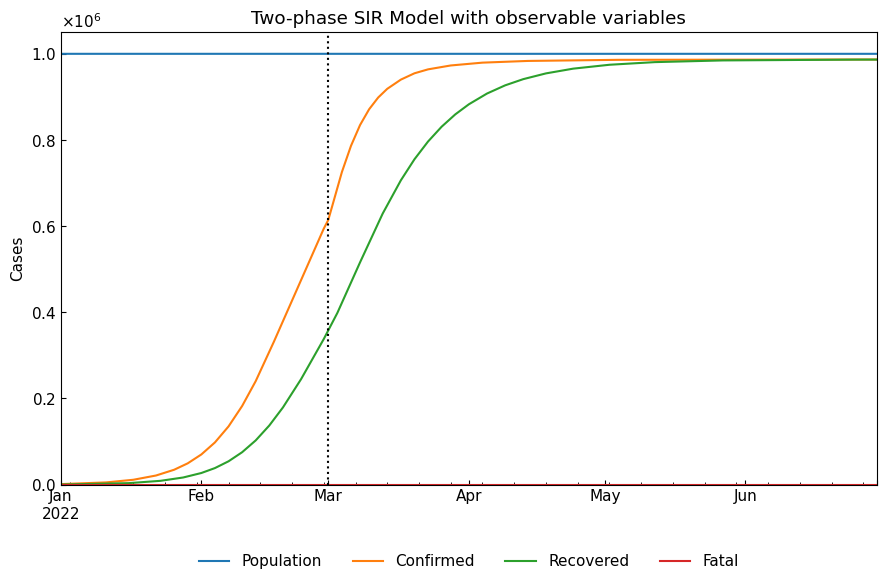
1-5. Observable variables

Actually, observable variables are Population/Confirmed/Infected/Recovered. We can calculate Population and Confirmed as follows.

  • Confirmed = Infected + Fatal + Recovered

  • Population = Susceptible + Confirmed

[12]:

real_df = dyn.simulate(model_specific=False)
real_df["Confirmed"] = real_df[["Infected", "Fatal", "Recovered"]].sum(axis=1)
real_df["Population"] = real_df[["Susceptible", "Confirmed"]].sum(axis=1)
real_df = real_df.loc[:, ["Population", "Confirmed", "Recovered", "Fatal"]]
cs.line_plot(real_df, title=f"Two-phase {dyn.model_name} with observable variables", v=dyn.start_dates()[1:])
_images/04_phase_dependent_26_0.png

2. S-R change point analysis

S-R change point analysis (S-R trend analysis) is a technique to find the change points of phases with actual time-series data.

2-1. S-R plane

Author of the Kaggle Notebook considered S-R plane. This idea (S-R plane) is from Balkew, Teshome Mogessie, “The SIR Model When S(t) is a Multi-Exponential Function.” (2010).Electronic Theses and Dissertations.Paper 1747. This is for simplest SIR model, but we can apply it to SIR-F model.

We will focus on the following equations of SIR-derived ODE models.

\begin{align*} & \frac{\mathrm{d}S}{\mathrm{d}T}= - \frac{\beta}{N} S I \\ & \frac{\mathrm{d}R}{\mathrm{d}T}= \gamma I \\ \end{align*}

When \(I > 0\), this leads to \begin{align*} & \frac{\mathrm{d}S}{\mathrm{d}R}= - \frac{\beta}{N \gamma} S \\ & \beta, \gamma, N: const. \end{align*}

Because \(S(0) = N\), \(S\) is a function of \(R\) as follows.

[13]:

S = sympy.symbols("S", cls=sympy.Function)
N, R  = sympy.symbols("N R", positive=True)
beta, gamma = sympy.symbols(r"\beta \gamma", positive=True)
dS = - beta / (N * gamma) * S(R)
sr = sympy.dsolve(S(R).diff(R) - dS, hint="separable", ics={S(0): N})
sr

[13]:
$\displaystyle S{\left(R \right)} = N e^{- \frac{R \beta}{N \gamma}}$

2-2. log(S) vs. R plane

Then,

[14]:

sympy.Eq(sympy.simplify(sympy.log(sr.lhs)), sympy.simplify(sympy.log(sr.rhs)))

[14]:
$\displaystyle \log{\left(S{\left(R \right)} \right)} = \log{\left(N \right)} - \frac{R \beta}{N \gamma}$

Where \(a=\cfrac{\beta}{N \gamma} \ (> 0)\), \begin{align*} & \log S_{(R)} = - a R + \log N \\ & N: const. \end{align*}

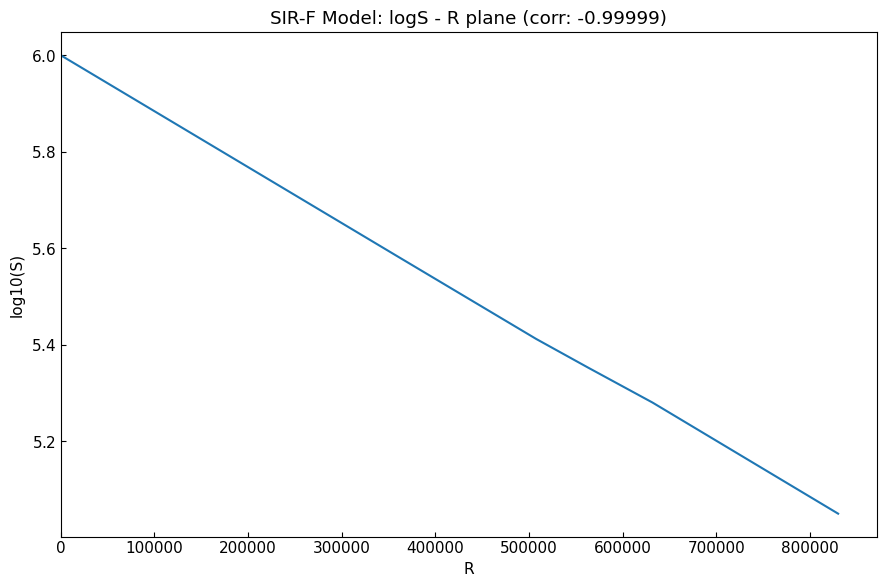
\(\log S\) decreases constantly with increase of \(R\), when the records follow a SIR-derived model and the parameter values of the model are constant. Plot of \((x, y) = (R, \log S)\) shows a line.

[15]:

model = deepcopy(cs.SIRFModel)
sirf = model.from_sample()
solved_df = sirf.solve()
sr_df = model.sr(model.inverse_transform(solved_df))
corr = sr_df["log10(S)"].corr(sr_df["R"]).round(5)
cs.line_plot(
    sr_df.set_index("R"),
    title=f"{model.name()}: logS - R plane (corr: {corr})",
    xlabel="R", xlim=(0, None),
    ylabel="log10(S)", ylim=(None, None),
    show_legend=False
)
_images/04_phase_dependent_37_0.png

Initial values on the first date was set, but the summary shows just a phase with no set ODE parameter values.

Limitations:
Because \(a=\cfrac{\beta}{N \gamma}\), the changes of \(\alpha_1\) and \(\alpha_2\) of SIR-D/SIR-F model cannot be detected.

2-3. Plane of phase-dependent models

Correlation coefficient is about -1.0 when ODE parameter values are constant The slope of the line may change when the ODE parameter values are changed.

Sample data of phase-dependent SIR-F model is here.

[16]:

dyn = cs.Dynamics.from_sample(cs.SIRFModel, date_range=("01Jan2022", "30Jun2022"))
# Set some phases by changing ODE parameter values
df = dyn.register()
parameters = ["theta", "kappa", "rho", "sigma"]
df.loc["18Feb2022", parameters] = [0.0002, 0.005, 0.40, 0.075]
df.loc["24Feb2022", parameters] = [0.0002, 0.005, 0.15, 0.075]
df.loc["01Mar2022", parameters] = [0.0002, 0.003, 0.40, 0.075]
df.loc["08Mar2022", parameters] = [0.0002, 0.005, 0.40, 0.150]
df.loc["15Mar2022", parameters] = [0.0000, 0.005, 0.40, 0.150]
dyn.register(df)
# Show summary
dyn.summary()[["Start", "End", "Rt", *parameters]].style.format(precision=4).background_gradient()

[16]:
  Start End Rt theta kappa rho sigma
Phase              
0th 2022-01-01 00:00:00 2022-02-17 00:00:00 2.5000 0.0020 0.0050 0.2000 0.0750
1st 2022-02-18 00:00:00 2022-02-23 00:00:00 5.0000 0.0002 0.0050 0.4000 0.0750
2nd 2022-02-24 00:00:00 2022-02-28 00:00:00 1.8700 0.0002 0.0050 0.1500 0.0750
3rd 2022-03-01 00:00:00 2022-03-07 00:00:00 5.1300 0.0002 0.0030 0.4000 0.0750
4th 2022-03-08 00:00:00 2022-03-14 00:00:00 2.5800 0.0002 0.0050 0.4000 0.1500
5th 2022-03-15 00:00:00 2022-06-30 00:00:00 2.5800 0.0000 0.0050 0.4000 0.1500

Dynamics:

[17]:

model = deepcopy(cs.SIRFModel)
df = dyn.simulate(model_specific=True)
cs.line_plot(
    df[["Susceptible", "Recovered"]],
    color_dict={"Susceptible": "blue", "Recovered": "green"},
    title=f"Phase-dependent {model.name()}: dynamics",
    v=dyn.start_dates()[1:],
    bbox_to_anchor=(0.5, -0.3), bbox_loc="lower center",
)
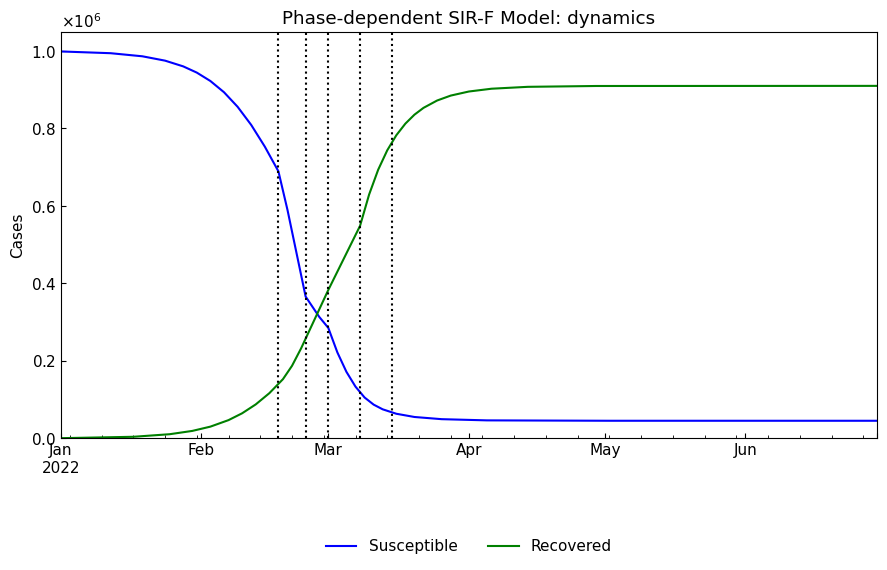
_images/04_phase_dependent_44_0.png

Plot of \((R, \log _{10} S)\): with vertical lines on change points (= start dates of phases 1st - last):

[18]:

model = deepcopy(cs.SIRFModel)
# Get (R, log10S)
sr_df = model.sr(dyn.simulate())
# Plotting
cs.line_plot(
    sr_df.set_index("R"),
    title=f"Phase-dependent {model.name()}: logS - R plane\nwith vertical lines on change points",
    xlabel="R", xlim=(0, None),
    ylabel="log10(S)", ylim=(None, None),
    show_legend=False,
    v=[sr_df.loc[d, "R"] for d in dyn.start_dates()[1:]],
)
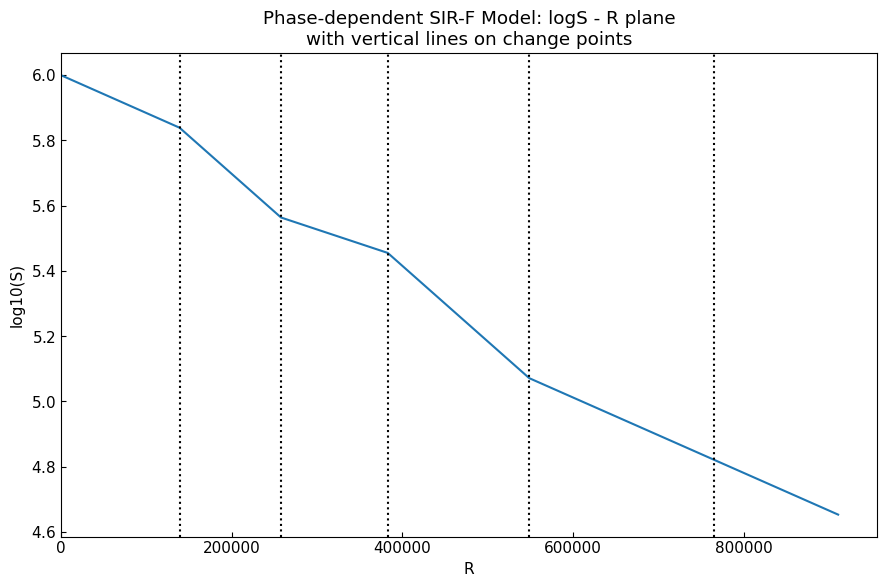
_images/04_phase_dependent_46_0.png

With the plotting, we can confirm most of the change points (except for 5th - 6th: difficult because the change was for \(\alpha_1\)).

2.4 Time-series segmentation

The previous sub-sections demonstrated that change points of S-R trend suggest change points of phases. Here, we will detect the change points of S-R trend with Dynamics().detect() via Dynamics.segment(). They uses ruptures library: change point detection in Python for off-line change point detection.

We will prepare a dataset which has the 0th - 5th phase.

[19]:

dyn = cs.Dynamics.from_sample(cs.SIRFModel, date_range=("01Jan2022", "30Jun2022"), tau=1440)
# Set some phases by changing ODE parameter values
df = dyn.register()
parameters = ["theta", "kappa", "rho", "sigma"]
df.loc["18Feb2022", parameters] = [0.0002, 0.005, 0.40, 0.075]
df.loc["24Feb2022", parameters] = [0.0002, 0.005, 0.15, 0.075]
df.loc["01Mar2022", parameters] = [0.0002, 0.003, 0.40, 0.075]
df.loc["08Mar2022", parameters] = [0.0002, 0.005, 0.40, 0.150]
df.loc["15Mar2022", parameters] = [0.0000, 0.005, 0.40, 0.150]
dyn.register(df)
# Simulation
sim_df = dyn.simulate(model_specific=False)
cs.line_plot(
    sim_df,
    title=f"Prepared dataset with phases and {dyn.model_name}",
    bbox_to_anchor=(0.5, -0.3),
)
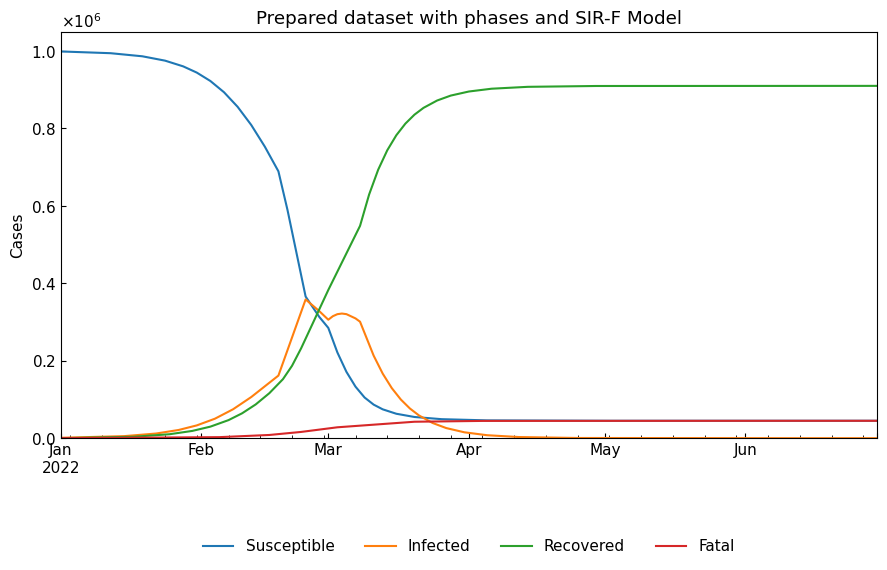
_images/04_phase_dependent_50_0.png

Create an instance of Dynamics with the prepared data. Note that the instance does not know the change points of phases.

[20]:

dyn_sim = cs.Dynamics.from_data(model=cs.SIRFModel, data=sim_df, tau=None, name="Sample data")
# Show summary
display(dyn_sim.summary())
Start End
Phase
0th 2022-01-01 2022-06-30

Dynamics().detect() performs S-R change point analysis (trend analysis) and show the trend on S-R plane. Dot lines are the change points of phases.

With algo argument, we can select the algorithm and models to detect the change points from “Binseg-normal” (default), “Pelt-rbf”, “Binseg-rbf”, “BottomUp-rbf”, “BottomUp-normal”. Please refer to the documentation of ruptures library.

Additionally, we can specify the minimum size of phases with argument min_size=7 (as default, [days]).

[21]:

points, fit_df = dyn_sim.detect(algo="Binseg-rbf", min_size=7)
# List of change points
pprint(points)
# Plotted values
display(fit_df)
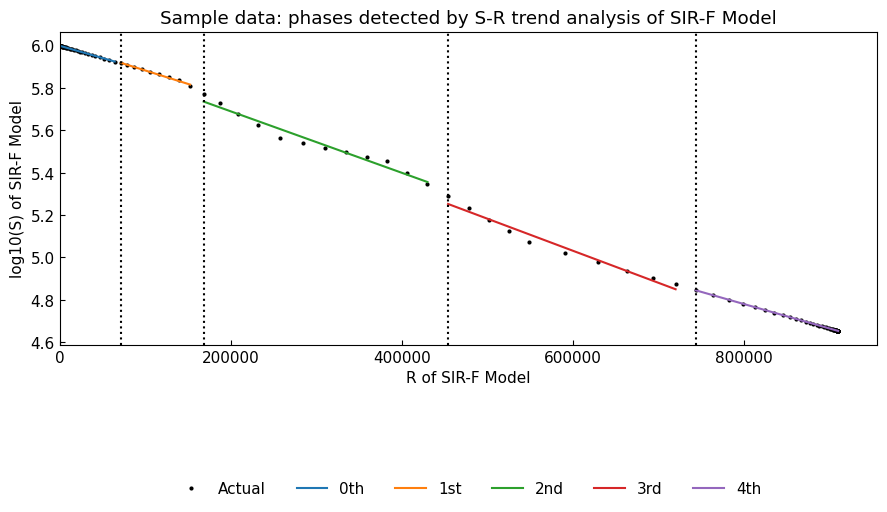
_images/04_phase_dependent_54_0.png 
[Timestamp('2022-02-11 00:00:00'),
 Timestamp('2022-02-20 00:00:00'),
 Timestamp('2022-03-04 00:00:00'),
 Timestamp('2022-03-14 00:00:00')]
Actual 0th 1st 2nd 3rd 4th Fitted
R
0 5.999565 5.999569 NaN NaN NaN NaN 5.999569
80 5.999473 5.999476 NaN NaN NaN NaN 5.999476
169 5.999369 5.999373 NaN NaN NaN NaN 5.999373
271 5.999252 5.999255 NaN NaN NaN NaN 5.999255
385 5.999120 5.999123 NaN NaN NaN NaN 5.999123
... ... ... ... ... ... ... ...
910075 4.652981 NaN NaN NaN NaN 4.652989 4.652989
910076 4.652981 NaN NaN NaN NaN 4.652988 4.652988
910077 4.652981 NaN NaN NaN NaN 4.652986 4.652986
910078 4.652981 NaN NaN NaN NaN 4.652985 4.652985
910079 4.652981 NaN NaN NaN NaN 4.652984 4.652984

153 rows × 7 columns

Note that detected phases are un-registered to the instance.

[22]:

dyn_sim.summary()

[22]:
Start End
Phase
0th 2022-01-01 2022-06-30

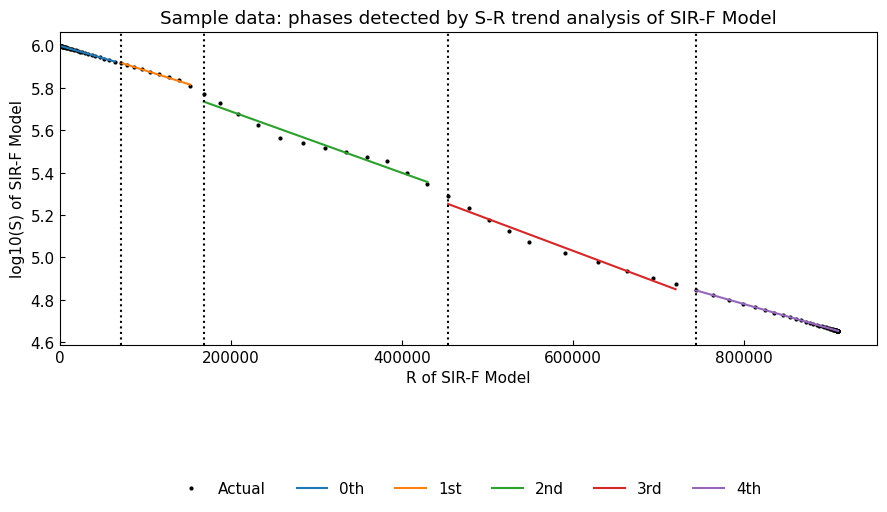
To perform time-series segmentation with S-R trend analysis, we will use Dynamics().segment(), which accepts all keyword arguments of Dynamics().detect().

[23]:

dyn_sim.segment(algo="Binseg-rbf", min_size=7)
# Show summary
dyn_sim.summary()
_images/04_phase_dependent_58_0.png 
[23]:
Start End
Phase
0th 2022-01-01 2022-02-10
1st 2022-02-11 2022-02-19
2nd 2022-02-20 2022-03-03
3rd 2022-03-04 2022-03-13
4th 2022-03-14 2022-06-30

If we need to add new change points or over-write change points, we will use Dynamics().segment(points=<list>, overwrite=<bool>).

[24]:

# Over-write
dyn_sim.segment(points=["01Mar2022", "01Jun2022"], overwrite=True)
# Add
dyn_sim.segment(points=["01May2022"], overwrite=False)
# Show summary
dyn_sim.summary()

[24]:
Start End
Phase
0th 2022-01-01 2022-02-28
1st 2022-03-01 2022-04-30
2nd 2022-05-01 2022-05-31
3rd 2022-06-01 2022-06-30

3. ODE parameter estimation

This section demonstrates how to estimate tau value (constant for all phases) and the ODE parameter values of phases.

3.1 Preparation

Create an Dynamics() instance which has a dataset with 6 phases (the 0th - 5th). The instance knows change points, but does not know tau value and ODE parameter values.

Create dataset.

[25]:

dyn = cs.Dynamics.from_sample(cs.SIRFModel, date_range=("01Jan2022", "30Jun2022"), tau=1440)
# Set some phases by changing ODE parameter values
df = dyn.register()
parameters = ["theta", "kappa", "rho", "sigma"]
df.loc["18Feb2022", parameters] = [0.0002, 0.005, 0.40, 0.075]
df.loc["24Feb2022", parameters] = [0.0002, 0.005, 0.15, 0.075]
df.loc["01Mar2022", parameters] = [0.0002, 0.003, 0.40, 0.075]
df.loc["08Mar2022", parameters] = [0.0002, 0.005, 0.40, 0.150]
df.loc["15Mar2022", parameters] = [0.0000, 0.005, 0.40, 0.150]
dyn.register(df)
# Simulation
sim_df = dyn.simulate(model_specific=False)
cs.line_plot(
    sim_df,
    title=f"Prepared dataset with phases and {dyn.model_name}",
    bbox_to_anchor=(0.5, -0.3),
)
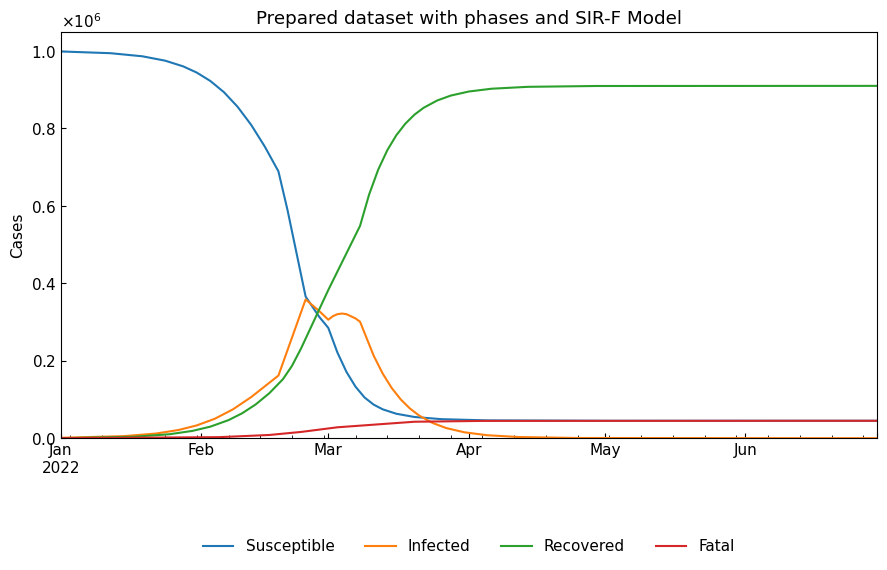
_images/04_phase_dependent_64_0.png

Create Dynamics() instance.

[26]:

dyn_est = cs.Dynamics.from_data(cs.SIRFModel, data=sim_df, tau=None, name="Sample data")
dyn_est.segment(points=["18Feb2022", "24Feb2022", "01Mar2022", "08Mar2022", "15Mar2022"])
# Show tau value
print(f"Tau value [min]: {dyn_est.tau or 'un-set'}")
# Show summary
display(dyn_est.summary())

Tau value [min]: un-set
Start End
Phase
0th 2022-01-01 2022-02-17
1st 2022-02-18 2022-02-23
2nd 2022-02-24 2022-02-28
3rd 2022-03-01 2022-03-07
4th 2022-03-08 2022-03-14
5th 2022-03-15 2022-06-30

3.2 Tau estimation

Before ODE parameter estimation, we need to select tau value [min]. Tau value is expected to be constant for all phases because tau value is a parameter used to convert actual time (with unit [min]) to time steps (without units) from divisors of 1440).

Dynamics().estimate_tau(metric="RMSLE", q=0.5, digits=None, n_jobs=None) (as default) sets the best tau value for the registered data, estimating ODE parameters with quantiles.

Arguments:

  • metric (str): metric name for scoring when selecting best tau value

  • q (float): the quantiles to compute, values between (0, 1)

  • digits (int or None): effective digits of ODE parameter values or None (skip rounding)

  • n_jobs (int or None): the number of parallel jobs or None (CPU count)

Metrics (selectable candidates of metric):

  • ME: maximum residual error

  • MAE: mean absolute error

  • MSE: mean square error

  • MSLE: mean squared logarithmic error

  • MAPE: mean absolute percentage error

  • RMSE: root mean squared error

  • RMSLE: root mean squared logarithmic error

  • R2: the coefficient of determination

For example, RMSLE score will be calculated with the following equation. \begin{align*} \mathrm{RMSLE} = \sqrt{\cfrac{1}{n}\sum_{i=1}^{n}(log_{10}(A_{i} + 1) - log_{10}(P_{i} + 1))^2} \end{align*} Where \(A\) is the observed (actual) values, \(P\) is estimated (predicted) values. Variables are \(S (i=1), I (i=2), R (i=3)\ \mathrm{and}\ F (i=n=4)\) for SIR-F model. When RMSLE score is low, hyperparameter estimation is highly accurate. Please refer to external sites, including Medium: What’s the Difference Between RMSE and RMSLE?.

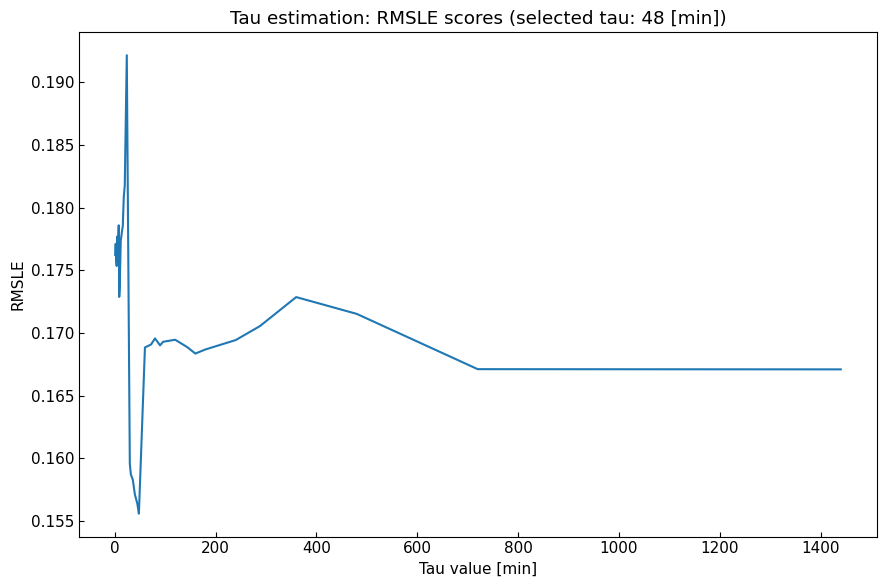
[27]:

metric = "RMSLE"
tau, score_df = dyn_est.estimate_tau(metric=metric)
print(f"Tau value [min]: {dyn_est.tau or 'un-set'}")
score_df.plot.line(
    title=f"Tau estimation: {metric} scores (selected tau: {tau} [min])",
    xlabel="Tau value [min]", ylabel=metric, legend=False
);

Tau value [min]: 48
_images/04_phase_dependent_68_1.png

3.3 ODE parameter estimation

Dynamics().estimate_params(metric="RMSLE", digits=None, n_jobs=None, **kwargs) (as default) sets ODE parameter values optimized for the registered data with hyperparameter optimization using Optuna library.

Arguments of Dynamics().estimate_params:

  • metric (str): metric name for scoring when optimizing ODE parameter values of phases

  • digits (int or None): effective digits of ODE parameter values or None (skip rounding)

  • n_jobs (int or None): the number of parallel jobs or None (CPU count)

  • **kwargs: keyword arguments of optimization

    • quantiles (tuple(int, int)): quantiles to cut parameter range, like confidence interval, (0.1, 0.9) as default

    • timeout (int): timeout of optimization, 180 as default

    • timeout_iteration (int): timeout of one iteration, 1 as default

    • tail_n (int): the number of iterations to decide whether score did not change for the last iterations, 4 as default

    • allowance (tuple(float, float)): the allowance of the max predicted values, (0.99, 1.01) as default

    • pruner (str): kind of pruner (hyperband, median, threshold or percentile), “threshold” as default

    • upper (float): works for “threshold” pruner, intermediate score is larger than this value, it prunes, 0.5 as default

    • percentile (float): works for “Percentile” pruner, the best intermediate value is in the bottom percentile among trials, it prunes, 50 as default

    • constant_liar (bool): whether use constant liar to reduce search effort or not, False as default

[28]:

est_df = dyn_est.estimate_params()
# Show RMSLE scores pf phases
est_df = est_df.drop_duplicates()
est_df.index.name = "Start"
display(est_df)

2024-10-03 at 13:15:33 | INFO | 
<SIR-F Model: parameter estimation>
2024-10-03 at 13:15:33 | INFO | Running optimization with 4 CPUs...

2024-10-03 at 13:16:00 | INFO | Completed optimization. Total: 0 min 27 sec
theta kappa rho sigma RMSLE Trials Runtime
Start
2022-01-01 0.000537 0.000176 0.006618 0.002462 0.010762 127 0 min 8 sec
2022-02-24 0.000056 0.000212 0.006508 0.00317 0.037947 203 0 min 9 sec
2022-03-01 0.000165 0.000115 0.016231 0.002884 0.054854 234 0 min 11 sec
2022-03-15 0.263358 0.000016 0.013188 0.004979 0.015927 107 0 min 9 sec
2022-03-08 0.000003 0.000205 0.016925 0.00611 0.061414 389 0 min 14 sec
2022-02-18 0.000117 0.000186 0.015258 0.002826 0.047217 623 0 min 27 sec 
[29]:

dyn_est.summary()

[29]:
Start End Rt theta kappa rho sigma alpha1 [-] 1/alpha2 [day] 1/beta [day] 1/gamma [day]
Phase
0th 2022-01-01 2022-02-17 2.51 0.000537 0.000176 0.006618 0.002462 0.001 189 5 14
1st 2022-02-18 2022-02-23 5.06 0.000117 0.000186 0.015258 0.002826 0.0 179 2 12
2nd 2022-02-24 2022-02-28 1.92 0.000056 0.000212 0.006508 0.00317 0.0 157 5 11
3rd 2022-03-01 2022-03-07 5.41 0.000165 0.000115 0.016231 0.002884 0.0 289 2 12
4th 2022-03-08 2022-03-14 2.68 0.000003 0.000205 0.016925 0.00611 0.0 163 2 5
5th 2022-03-15 2022-06-30 1.94 0.263358 0.000016 0.013188 0.004979 0.263 2107 3 7

4. With actual data

This section demonstrates how to divide actual time-series data with phases (“S-R change point analysis”) and to estimate ODE parameter values of phases (“ODE parameter estimation”).

4-1. Data preparation

Prepare actual prefecture-level time-series data in Japan for demonstration.

Download the dataset.

[30]:

eng = cs.DataEngineer()
eng.download(country=None, databases=["japan", "covid19dh"]);

Data cleaning, transformation, subsetting, complement.

[31]:

eng.clean()
eng.transform()
actual_df, status, _ = eng.subset(geo=("Japan",), variables="SIRF", complement=True)
print(status)
actual_df.tail()

monotonic increasing complemented confirmed data and
monotonic increasing complemented fatal data and
fully complemented recovered data

[31]:
Susceptible Infected Recovered Fatal
Date
2023-05-04 92738009.0 183209 33533260 74622
2023-05-05 92732198.0 177397 33544864 74641
2023-05-06 92725964.0 171546 33556937 74653
2023-05-07 92711524.0 175456 33567458 74662
2023-05-08 92702197.0 174762 33577464 74677

Plotting: removed “Susceptible” from the figure because “Susceptible” >> max(“Infected”, “Infected”, “Recovered”).

[32]:

cs.line_plot(actual_df.drop("Susceptible", axis=1), "Actual data in Japan")
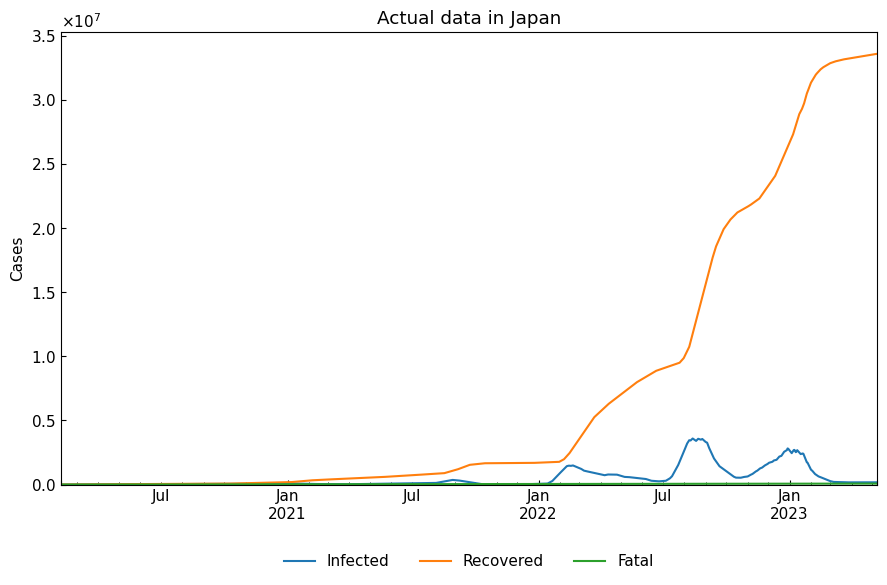
_images/04_phase_dependent_79_0.png

With the data, create an instance of Dynamics class.

[33]:

dyn_act = cs.Dynamics.from_data(model=cs.SIRFModel, data=actual_df, name="Japan")
# Show registered values
dyn_act.register().tail()

[33]:
Susceptible Infected Recovered Fatal theta kappa rho sigma
Date
2023-05-04 92738009.0 183209.0 33533260.0 74622.0 <NA> <NA> <NA> <NA>
2023-05-05 92732198.0 177397.0 33544864.0 74641.0 <NA> <NA> <NA> <NA>
2023-05-06 92725964.0 171546.0 33556937.0 74653.0 <NA> <NA> <NA> <NA>
2023-05-07 92711524.0 175456.0 33567458.0 74662.0 <NA> <NA> <NA> <NA>
2023-05-08 92702197.0 174762.0 33577464.0 74677.0 <NA> <NA> <NA> <NA> 
[34]:

# Show summary
dyn_act.summary()

[34]:
Start End
Phase
0th 2020-02-06 2023-05-08

4-2. Time-series segmentation

With Dynamics.segment(), we will apply S-R change point analysis (trend analysis) to the prepared actual data.

[35]:

dyn_act.segment();
# Show summary
dyn_act.summary().T
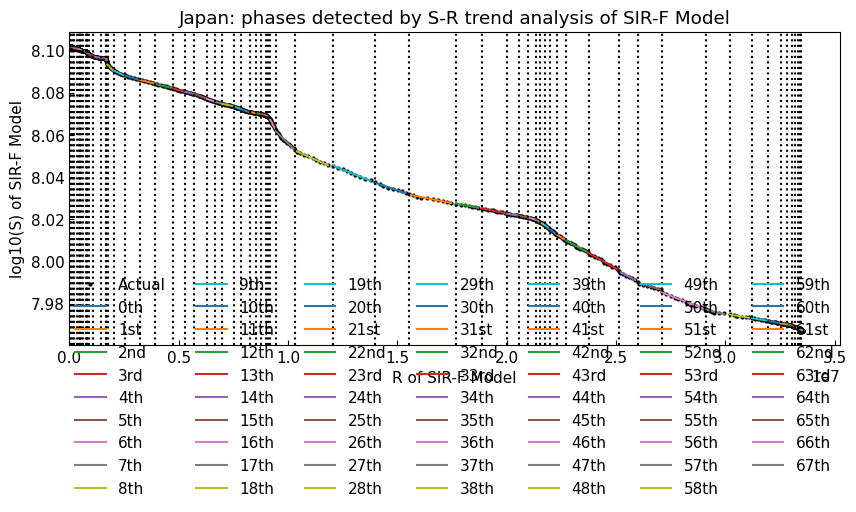
_images/04_phase_dependent_84_0.png 
[35]:
Phase 0th 1st 2nd 3rd 4th 5th 6th 7th 8th 9th ... 58th 59th 60th 61st 62nd 63rd 64th 65th 66th 67th
Start 2020-02-06 2020-08-11 2020-11-17 2020-12-25 2021-01-17 2021-02-11 2021-04-04 2021-04-22 2021-05-07 2021-05-25 ... 2023-01-24 2023-01-31 2023-02-08 2023-02-20 2023-03-01 2023-03-13 2023-03-28 2023-04-08 2023-04-19 2023-04-28
End 2020-08-10 2020-11-16 2020-12-24 2021-01-16 2021-02-10 2021-04-03 2021-04-21 2021-05-06 2021-05-24 2021-07-01 ... 2023-01-30 2023-02-07 2023-02-19 2023-02-28 2023-03-12 2023-03-27 2023-04-07 2023-04-18 2023-04-27 2023-05-08

2 rows × 68 columns

4-3. Parameter estimation

Dynamics().estimate(**kwargs) performs Dynamics().estimate_tau() and Dynamics().estimate_params() in order.

[36]:

dyn_act.estimate()
print(f"Tau value [min]: {dyn_act.tau or 'un-set'}")
# Show summary
dyn_act.summary()

2024-10-03 at 13:16:51 | INFO | 
<SIR-F Model: parameter estimation>
2024-10-03 at 13:16:51 | INFO | Running optimization with 4 CPUs...

2024-10-03 at 13:16:51 | INFO | Running optimization with 4 CPUs...
2024-10-03 at 13:19:20 | INFO | Completed optimization. Total: 2 min 29 sec

Tau value [min]: 15

[36]:
Start End Rt theta kappa rho sigma alpha1 [-] 1/alpha2 [day] 1/beta [day] 1/gamma [day]
Phase
0th 2020-02-06 2020-08-10 1.5 0.021396 0.000051 0.00117 0.000712 0.021 204 9 15
1st 2020-08-11 2020-11-16 0.89 0.003129 0.000008 0.000747 0.000831 0.003 1343 14 13
2nd 2020-11-17 2020-12-24 1.74 0.000366 0.000008 0.000755 0.000426 0.0 1359 14 24
3rd 2020-12-25 2021-01-16 1.54 0.001955 0.000007 0.000782 0.0005 0.002 1498 13 21
4th 2021-01-17 2021-02-10 0.69 0.002807 0.00001 0.000445 0.000638 0.003 993 23 16
... ... ... ... ... ... ... ... ... ... ... ...
63rd 2023-03-13 2023-03-27 1.83 0.000503 0.000002 0.000704 0.000383 0.001 6296 15 27
64th 2023-03-28 2023-04-07 0.66 0.000217 0.000002 0.000674 0.001014 0.0 4528 15 10
65th 2023-04-08 2023-04-18 1.47 0.002585 0.000001 0.001081 0.000732 0.003 8188 10 14
66th 2023-04-19 2023-04-27 1.81 0.000954 0.000002 0.000878 0.000483 0.001 6782 12 22
67th 2023-04-28 2023-05-08 1.57 0.000112 0.000001 0.000951 0.000604 0.0 7027 11 17

68 rows × 11 columns

4-4. Accuracy evaluation

Compare the simulated results and actual records, and evaluate the differences.

Arguments: - date_range (tuple of (str or pandas.Timestamp or None) or None): range of dates to evaluate or None (the first and the last date) - metric (str): metric to evaluate the difference, “RMSLE” as default - display (bool): whether display figure of comparison or not - kwargs: keyword arguments of covsirphy.compare_plot()

[37]:

metric = "RMSLE"
score = dyn_act.evaluate(metric=metric)
print(f"{metric}: {score:.4} (overall score for time-series segmentation, tau estimation and ODE parameter estimation)")
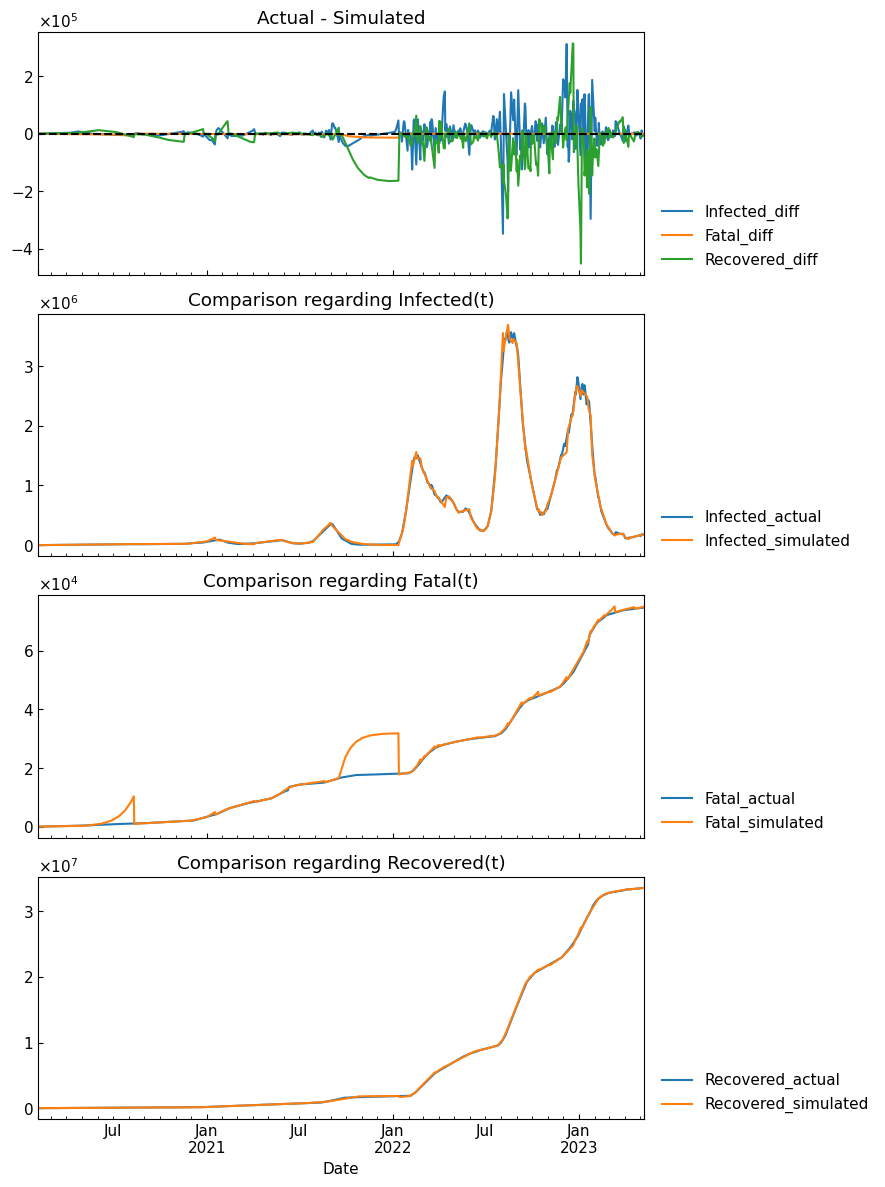
_images/04_phase_dependent_88_0.png 
RMSLE: 0.5651 (overall score for time-series segmentation, tau estimation and ODE parameter estimation)

4-5. Simulation

Simulate the dynamics with the estimated parameter sets of phases.

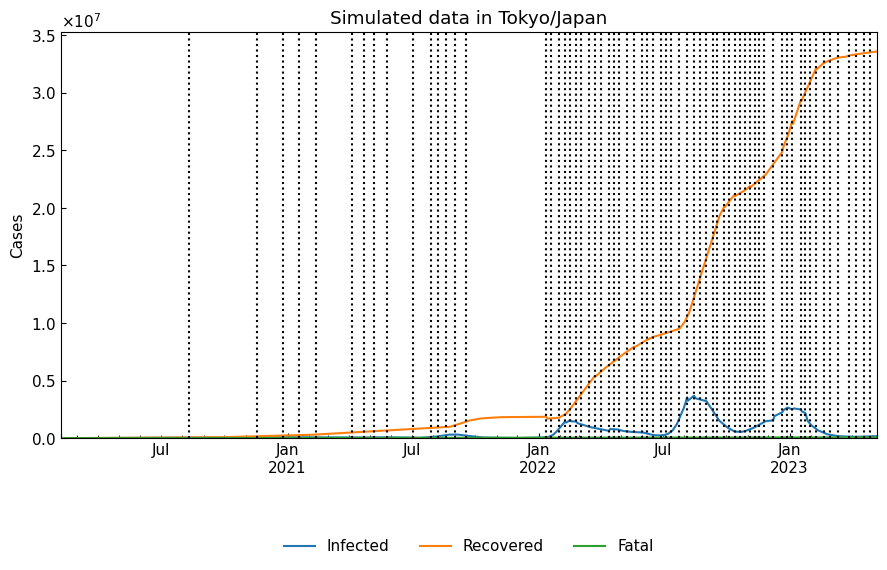
[38]:

simulated_df = dyn_act.simulate()

[39]:

cs.line_plot(
    simulated_df.drop("Susceptible", axis=1),
    title="Simulated data in Tokyo/Japan",
    v=dyn_act.start_dates()[1:],
    bbox_to_anchor=(0.5, -0.3),
)
_images/04_phase_dependent_91_0.png

When we need to simulate for the last 30 days, we can use Dynamics().parse_days(days=-30, ref="last").

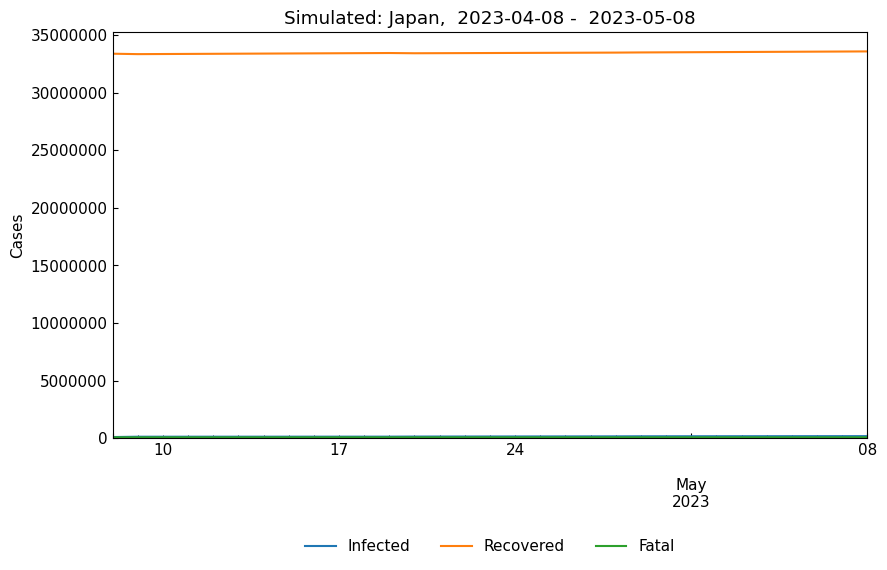
[40]:

start, end = dyn_act.parse_days(days=-30, ref="last")
cs.line_plot(
    simulated_df.drop("Susceptible", axis=1).loc[start: end],
    title=f"Simulated: Japan, {start: %Y-%m-%d} - {end: %Y-%m-%d}",
    bbox_to_anchor=(0.5, -0.3),
    y_integer=True,
)
_images/04_phase_dependent_93_0.png

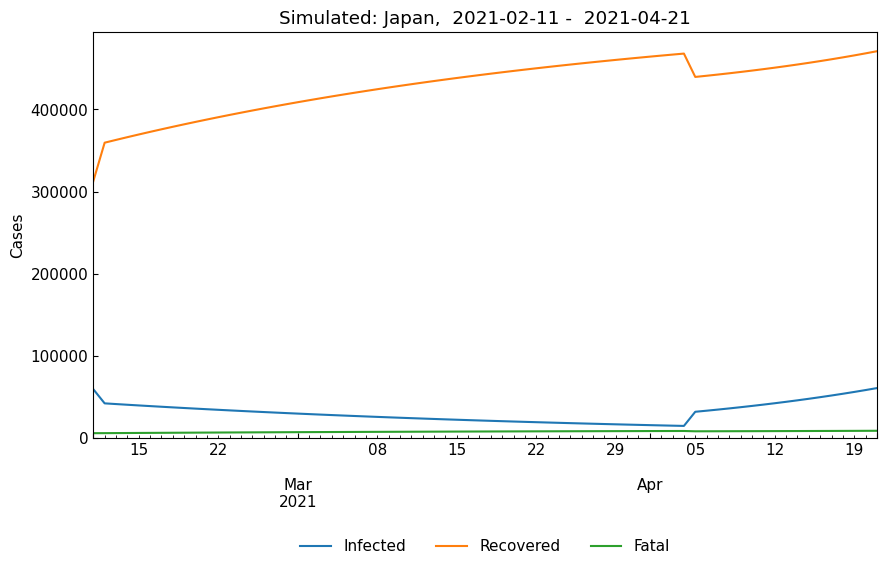
When we need to perform simulation for th 5th and 6th phase, We can use Dynamics().parse_phases(phases=["5th", "6th"])).

[41]:

start, end = dyn_act.parse_phases(phases=["5th", "6th"])
cs.line_plot(
    simulated_df.drop("Susceptible", axis=1).loc[start: end],
    title=f"Simulated: Japan, {start: %Y-%m-%d} - {end: %Y-%m-%d}",
    bbox_to_anchor=(0.5, -0.3),
    y_integer=True,
)
_images/04_phase_dependent_95_0.png

4-6. Tracking of ODE parameters

Track the estimated ODE parameter values.

[42]:

track_df = dyn_act.track()
track_df.tail()

[42]:
Rt theta kappa rho sigma alpha1 [-] 1/alpha2 [day] 1/beta [day] 1/gamma [day]
Date
2023-05-04 1.57 0.000112 0.000001 0.000951 0.000604 0.0 7027 11 17
2023-05-05 1.57 0.000112 0.000001 0.000951 0.000604 0.0 7027 11 17
2023-05-06 1.57 0.000112 0.000001 0.000951 0.000604 0.0 7027 11 17
2023-05-07 1.57 0.000112 0.000001 0.000951 0.000604 0.0 7027 11 17
2023-05-08 1.57 0.000112 0.000001 0.000951 0.000604 0.0 7027 11 17 
[43]:

track_df.columns

[43]:

Index(['Rt', 'theta', 'kappa', 'rho', 'sigma', 'alpha1 [-]', '1/alpha2 [day]',
       '1/beta [day]', '1/gamma [day]'],
      dtype='object')

[44]:

def history(param_name, title=None, h=None):
    """Display the history of ODE parameter values tracked with global `track_df`.

    Args:
        param_name (str): name of the parameter
        title (str or None): figure title or Nome (@param_name will be used)
        h (list/tuple[int/float] or None): list of y values of horizontal lines or None
    """
    global track_df
    cs.line_plot(
        track_df.loc[:, param_name],
        title=title or f"Tracked {param_name}",
        ylabel=param_name,
        math_scale=False,
        h=h,
        show_legend=False,
    )
\(\theta\) and \(\alpha_1\):
Enhancement of PCR tests suppressed the number of fatal cases before confirmation.
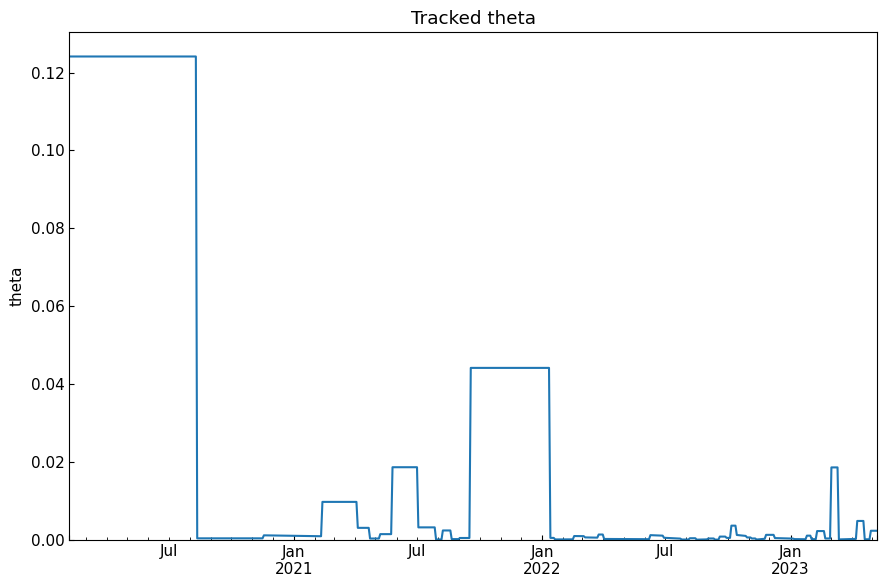
[45]:

history("theta")
_images/04_phase_dependent_101_0.png 
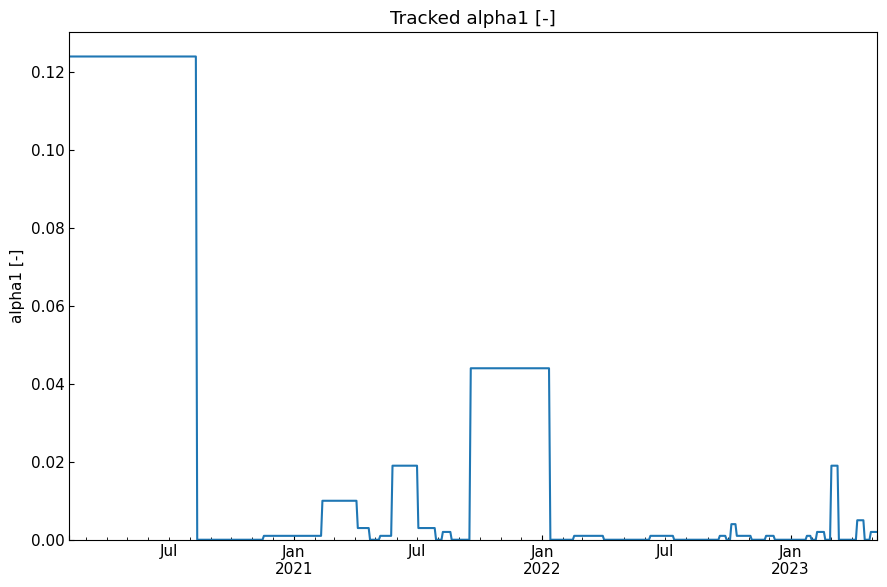
[46]:

history("alpha1 [-]")
_images/04_phase_dependent_102_0.png
\(\kappa\) and \(1/\alpha_2\):
Enhancement of medical system suppressed the number of fatal cases.
[47]:

history("kappa")
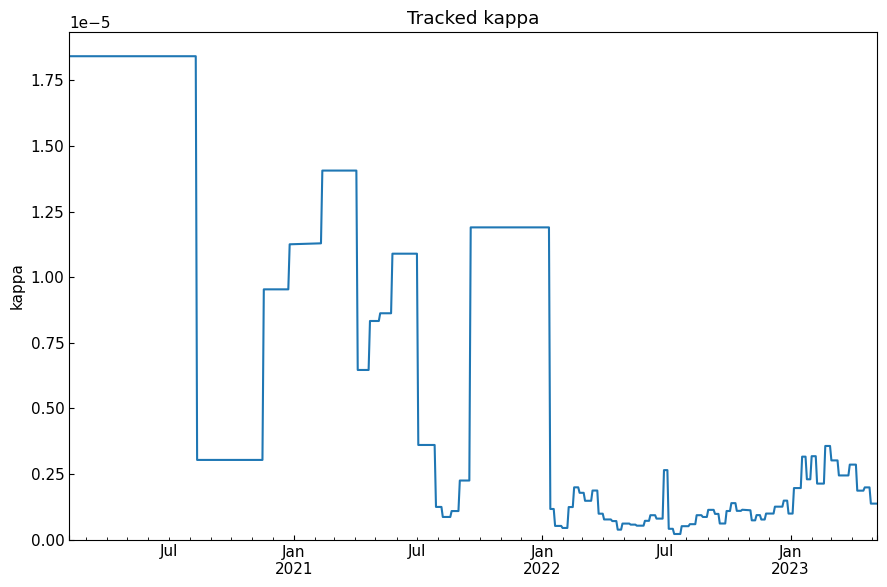
_images/04_phase_dependent_104_0.png 
[48]:

history("1/alpha2 [day]")
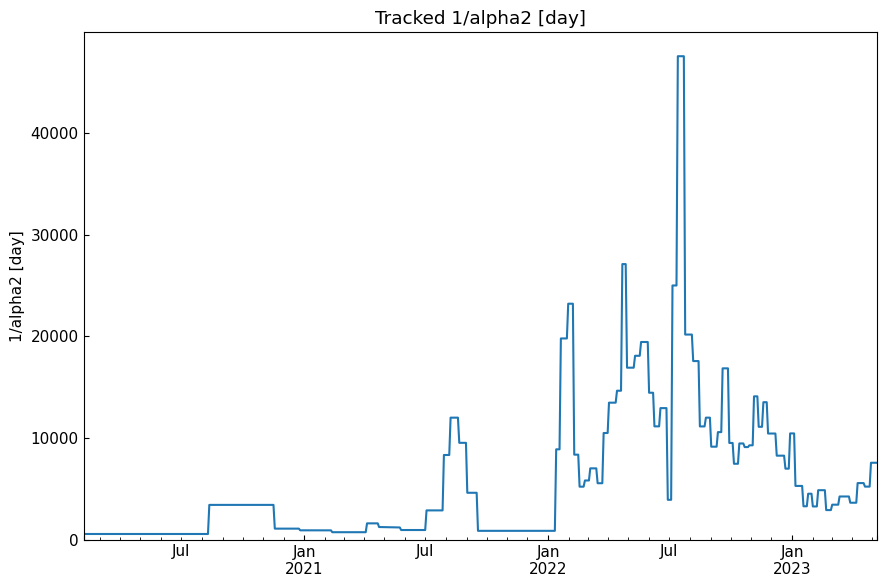
_images/04_phase_dependent_105_0.png
\(\rho\) and \(1/\beta\):
Contact rate was changed with emergency declaration in Tokyo.
[49]:

history("rho")
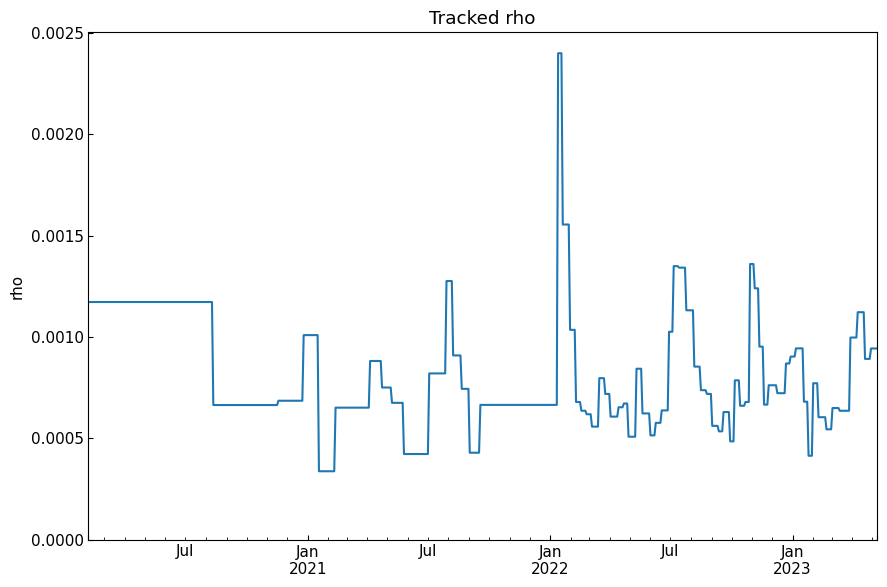
_images/04_phase_dependent_107_0.png 
[50]:

history("1/beta [day]")
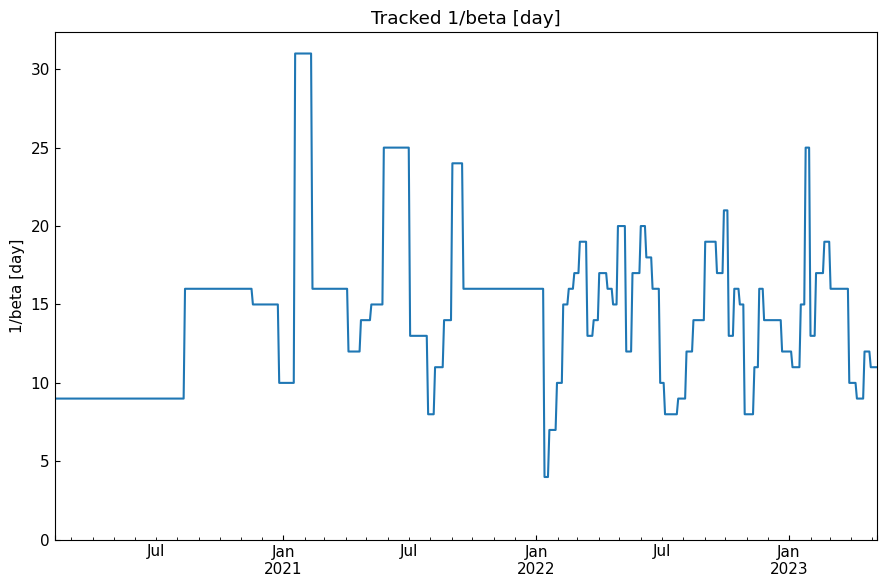
_images/04_phase_dependent_108_0.png
\(\sigma\) and \(1/\gamma\):
Recovery period is not changed clearly at this time.
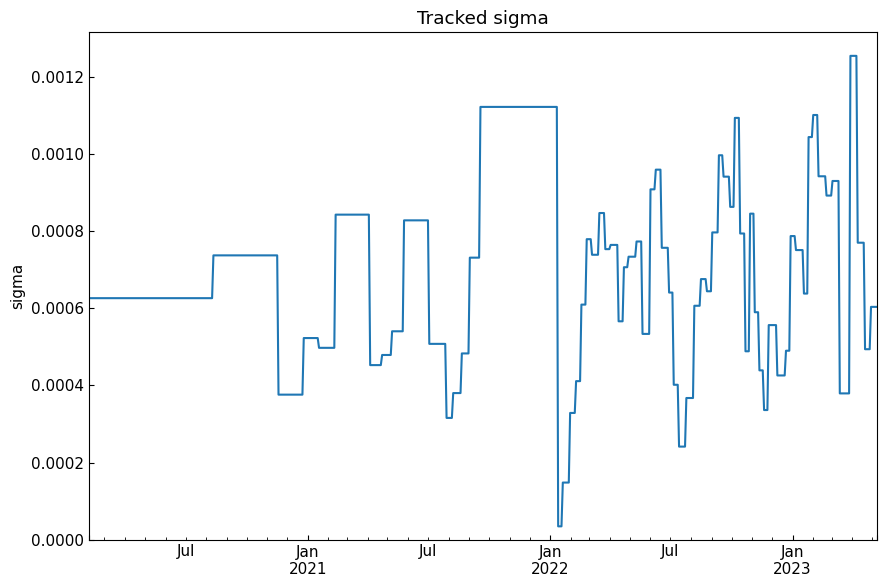
[51]:

history("sigma")
_images/04_phase_dependent_110_0.png 
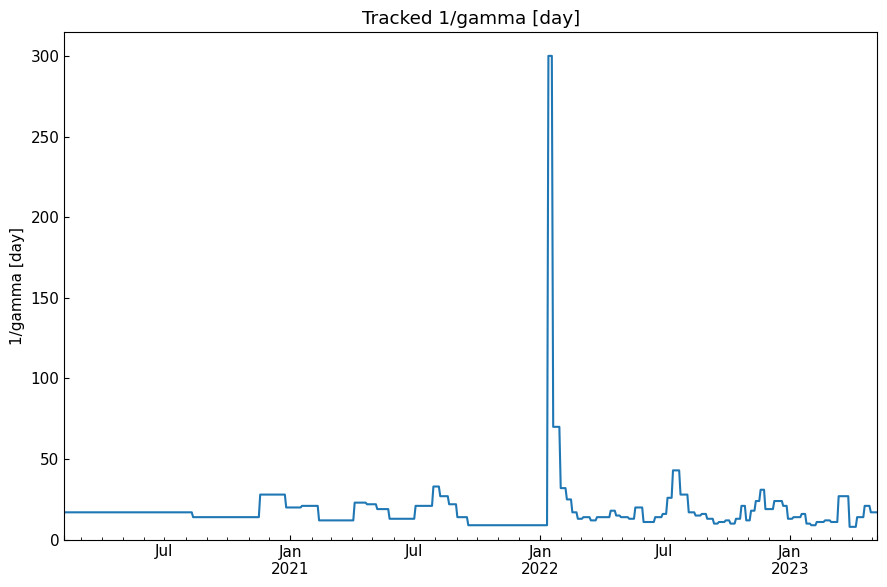
[52]:

history("1/gamma [day]")
_images/04_phase_dependent_111_0.png
Reproduction number:
Rt > 1 means explosive outbreak.
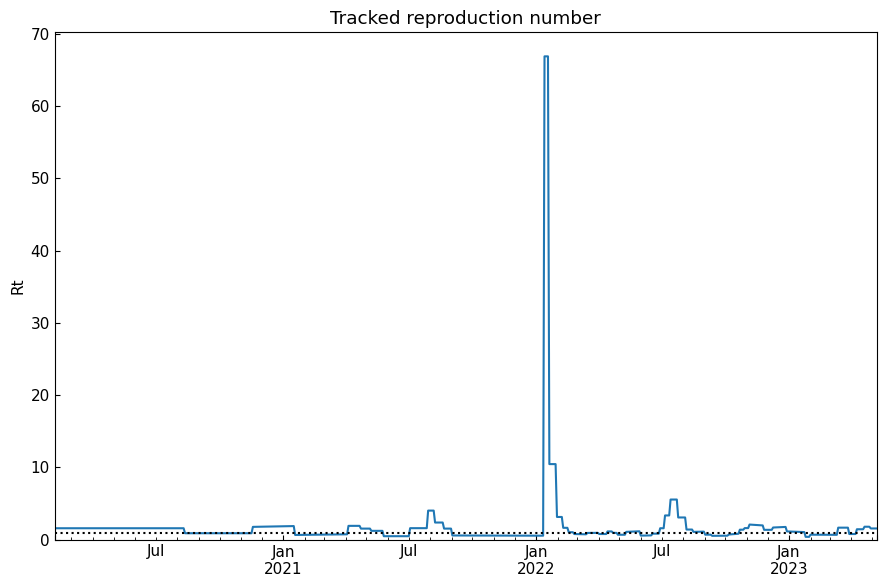
[53]:

history("Rt", title="Tracked reproduction number", h=1.0)
_images/04_phase_dependent_113_0.png

Thank you!