SIR-derived ODE models
SIR-derived ODE (ordinary differential equation) models are used in epidemiology. They are also named as compartment models and useful to understand the dynamics of outbreak of infectious diseases, including COVID-19.
Mathematical model enables us to describe complicated systems with some parameters simply. So, we can study how to predict and end the outbreak in epidemiology.
[1]:
from copy import deepcopy
from pprint import pprint
import covsirphy as cs
import numpy as np
cs.__version__
[1]:
'3.1.2.delta'
1. SIR model
SIR model is the simplest mathematical model with ODEs. Population is assigned to compartments named as follows.
Let’s start with the simplest SIR model proposed by Kermack, W. O., & McKendrick, A. G. (1927). Population is assigned to some compartments. “Susceptible people” may meet “Infected” patients and may be confirmed as “Infected”. “Infected” patients will move to “Removed (Recovered or Fatal)” compartment later.
1-1. Definition
\begin{align*} \mathrm{S} \overset{\beta I}{\longrightarrow} \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\ \end{align*}
Variables:
\(\mathrm{S}\): Susceptible (= Population - Confirmed)
\(\mathrm{I}\): Infected (=Confirmed - Recovered - Fatal)
\(\mathrm{R}\): Recovered or Fatal (= Recovered + Fatal)
Parameters:
\(\beta\): Effective contact rate \(\mathrm{[1/min]}\)
\(\gamma\): Recovery (+ Mortality) rate \(\mathrm{[1/min]}\)
1-2. Non-dimensional SIR model
To simplify the model, we will remove the units of the variables from the ODE model.
Set \((S, I, R) = N \times (x, y, z)\) and \((T, \beta, \gamma) = (\tau t, \tau^{-1} \rho, \tau^{-1} \sigma)\).
Where \(N\) is the total population and \(\tau\) is a coefficient ([min], is an integer to simplify).
1-3. Create sample data
We use SIRModel class, a child class of ODEModel. They have class method .from_sample(date_range=None, tau=1440) (as default) and this method creates an instance with preset parameter values and initial values of variables.
[2]:
sir = cs.SIRModel.from_sample()
repr(sir)
[2]:
"SIRModel(date_range=('15Dec2025', '13Jun2026'), tau=1440, initial_dict={'Susceptible': 999000, 'Infected': 1000, 'Fatal or Recovered': 0}, param_dict={'rho': 0.2, 'sigma': 0.075})"
We can specify the start/end date of dynamics and tau value as follows. Note that tau value [min] should be a divisor of 1440 to simplify operations.
[3]:
cs.SIRModel.from_sample(date_range=("01Jan2022", "31Dec2022"), tau=720)
[3]:
SIRModel(date_range=('01Jan2022', '31Dec2022'), tau=720, initial_dict={'Susceptible': 999000, 'Infected': 1000, 'Fatal or Recovered': 0}, param_dict={'rho': 0.2, 'sigma': 0.075})
When we need to change the values of arguments, create an instance directly with the class.
[4]:
cs.SIRModel(
date_range=('01Jan2022', '31Dec2022'),
tau=720,
initial_dict={'Susceptible': 995_000, 'Infected': 4_000, 'Fatal or Recovered': 1_000},
param_dict={'rho': 0.4, 'sigma': 0.075}
)
[4]:
SIRModel(date_range=('01Jan2022', '31Dec2022'), tau=720, initial_dict={'Susceptible': 995000, 'Infected': 4000, 'Fatal or Recovered': 1000}, param_dict={'rho': 0.4, 'sigma': 0.075})
We can also confirm the settings and definitions of the instance with instance method ODEModel().settings() and class method ODEModel.definition().
[5]:
pprint(sir.settings())
{'date_range': ('15Dec2025', '13Jun2026'),
'initial_dict': {'Fatal or Recovered': 0,
'Infected': 1000,
'Susceptible': 999000},
'param_dict': {'rho': 0.2, 'sigma': 0.075},
'tau': 1440}
[6]:
# pprint(cs.SIRModel.definitions())
pprint(sir.definitions())
{'dimensional_parameters': ['1/beta [day]', '1/gamma [day]'],
'name': 'SIR Model',
'parameters': ['rho', 'sigma'],
'variables': ['Susceptible', 'Infected', 'Fatal or Recovered']}
We can calculate dimensional parameter values with ODEModel().dimensional_parameters().
[7]:
sir.dimensional_parameters()
[7]:
{'1/beta [day]': 5, '1/gamma [day]': 13}
1-4. Solve ODEs
We can solve the ODEs with ODEModel().solve().
[8]:
sir_df = sir.solve()
sir_df.tail()
[8]:
| Susceptible | Infected | Fatal or Recovered | |
|---|---|---|---|
| Date | |||
| 2026-06-09 | 88354 | 750 | 910895 |
| 2026-06-10 | 88342 | 708 | 910950 |
| 2026-06-11 | 88329 | 669 | 911002 |
| 2026-06-12 | 88318 | 632 | 911050 |
| 2026-06-13 | 88307 | 596 | 911096 |
[9]:
cs.line_plot(sir_df, title=f"Sample data of {sir}", y_integer=True)
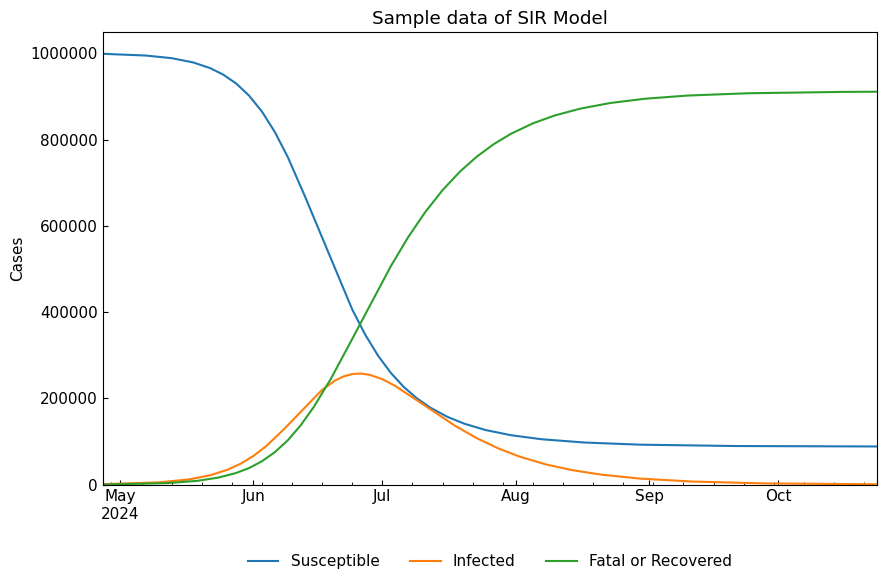
1-5. Reproduction number
Reproduction number of SIR model is defined as follows.
\begin{align*} R_0 = \rho \sigma^{-1} = \beta \gamma^{-1} \end{align*}
\(R_0\) (“R naught”) means “the average number of secondary infections caused by an infected host” (external link: Infection Modeling — Part 1).
We can calculate reproduction number using ODEModel().r0() method.
[10]:
sir.r0()
[10]:
2.67
[11]:
model = deepcopy(sir)
df = sir_df.copy()
# Calculate R0
r0 = model.r0()
# Prepare non-dimensional values
tau = model.settings()["tau"]
df.index = ((df.index - df.index.min()) / np.timedelta64(1440, "m")).astype(np.int64)
df.index.name = "t"
population = sum(model.settings()["initial_dict"].values())
df["x"] = df["Susceptible"] / population
df["y"] = df["Infected"] / population
# t for x = 1/R0
t0 = np.argmin(np.abs(df["x"] - 1/r0))
# y when x = 1/R0
y0 = df.loc[t0, "y"]
# Show x, y for t
cs.line_plot(
df[["x", "y"]],
title=f"{model} with R0 = {r0}: x, y for t (vertical line: t when x = 1/R0)", xlabel="t", math_scale=False, ylabel=None,
h=[1/r0, y0], v=t0,
bbox_to_anchor=None, bbox_loc="upper right", ncol=1,
)
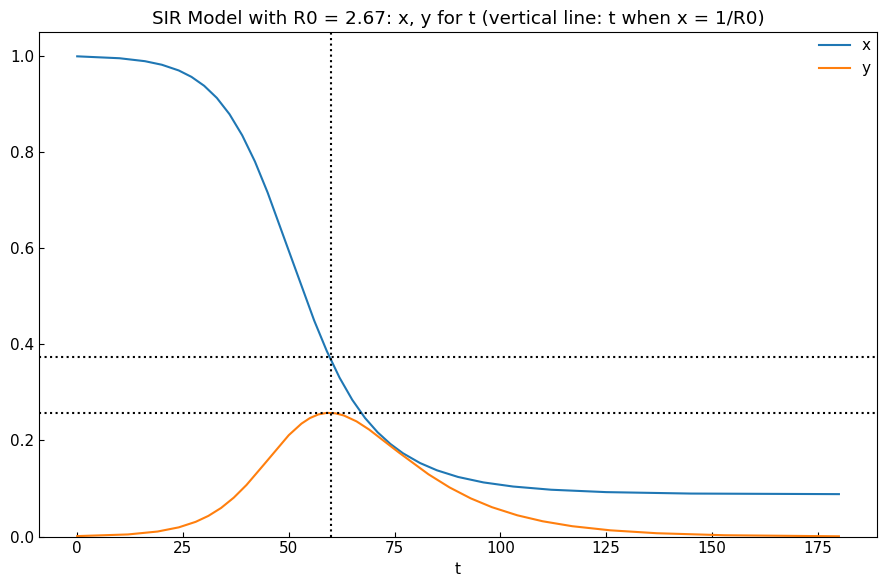
2. SIR-D model
Because we are measuring the number of fatal cases and recovered cases separately, we can use two variables (“Recovered” and “Deaths”) instead of “Recovered + Deaths” in the mathematical model. We call this model as SIR-D model.
2-1. Definition
\begin{align*} \mathrm{S} \overset{\beta I}{\longrightarrow}\ & \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\ & \mathrm{I} \overset{\alpha}{\longrightarrow} \mathrm{D} \\ \end{align*}
Variables:
\(\mathrm{S}\): Susceptible (= Population - Confirmed)
\(\mathrm{I}\): Infected (=Confirmed - Recovered - Fatal)
\(\mathrm{R}\): Recovered
\(\mathrm{D}\): Fatal
Parameters:
\(\alpha\): Mortality rate \(\mathrm{[1/min]}\)
\(\beta\): Effective contact rate \(\mathrm{[1/min]}\)
\(\gamma\): Recovery rate \(\mathrm{[1/min]}\)
2-2. Non-dimensional SIR-D model
2-3. Create sample data
We use SIRDModel class, a child class of ODEModel. They have class method .from_sample(date_range=None, tau=1440) (as default).
[12]:
sird = cs.SIRDModel.from_sample()
repr(sird)
[12]:
"SIRDModel(date_range=('15Dec2025', '13Jun2026'), tau=1440, initial_dict={'Susceptible': 999000, 'Infected': 1000, 'Recovered': 0, 'Fatal': 0}, param_dict={'kappa': 0.005, 'rho': 0.2, 'sigma': 0.075})"
2-4. Solve ODEs
We can solve the ODEs with ODEModel().solve().
[13]:
sird_df = sird.solve()
cs.line_plot(sird_df, title=f"Sample data of {sird}", y_integer=True)
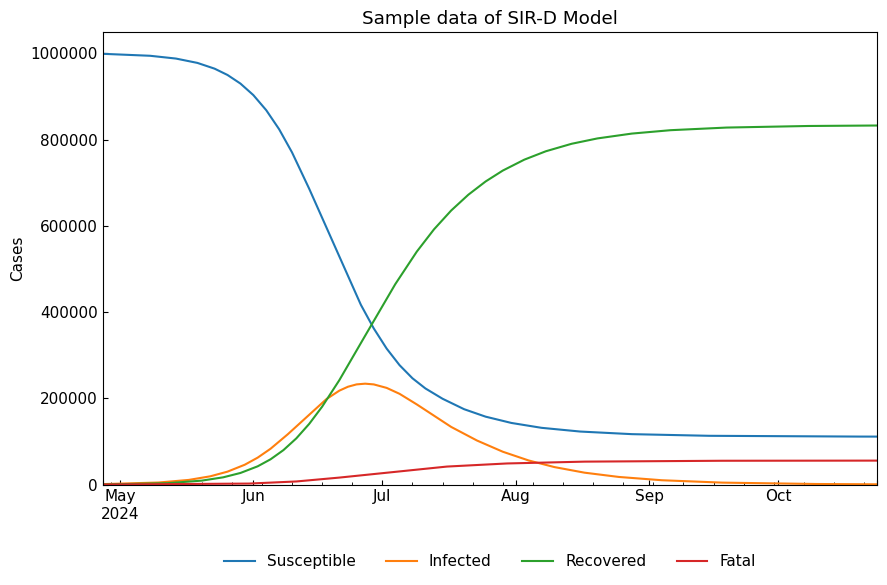
2-5. Reproduction number
Reproduction number of SIR-D model is defined as follows.
\begin{align*} R_0 = \rho (\sigma + \kappa)^{-1} = \beta (\gamma + \alpha)^{-1} \end{align*}
[14]:
sird.r0()
[14]:
2.5
3. SIR-F model
In the initial phase of COVID-19 outbreak, many cases were confirmed after they died. To consider this issue, “S + I \(\to\) Fatal + I” should be added. We call the next model as SIR-F model. This is an original model of CovsirPhy. When \(\alpha_{1}=0\), no difference with the SIR-D model.
SIR-F model was developed with Kaggle: COVID-19 data with SIR model.
3-1. Definition
\begin{align*} \mathrm{S} \overset{\beta I}{\longrightarrow} \mathrm{S}^\ast \overset{\alpha_1}{\longrightarrow}\ & \mathrm{F} \\ \mathrm{S}^\ast \overset{1 - \alpha_1}{\longrightarrow}\ & \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\ & \mathrm{I} \overset{\alpha_2}{\longrightarrow} \mathrm{F} \\ \end{align*}
Variables:
\(\mathrm{S}\): Susceptible (= Population - Confirmed)
\(\mathrm{S}^\ast\): Confirmed and un-categorized
\(\mathrm{I}\): Confirmed and categorized as Infected
\(\mathrm{R}\): Confirmed and categorized as Recovered
\(\mathrm{F}\): Confirmed and categorized as Fatal
Parameters:
\(\alpha_1\): Direct fatality probability of \(\mathrm{S}^\ast\) (non-dimensional)
\(\alpha_2\): Mortality rate of Infected cases \(\mathrm{[1/min]}\)
\(\beta\): Effective contact rate \(\mathrm{[1/min]}\)
\(\gamma\): Recovery rate \(\mathrm{[1/min]}\)
In JHU-style dataset, we know the number of cases who were confirmed with COVID-19, but we do not know the number of died cases who died without COVID-19. Essentially \(\mathrm{S}^\ast\) serves as an auxiliary compartment in SIR-F model to separate the two death situations and insert a probability factor of {\(\alpha_1\), \(1 - \alpha_1\)}.
3-2. Non-dimensional SIR-F model
3-3. Create sample data
We use SIRFModel class, a child class of ODEModel. They have class method .from_sample(date_range=None, tau=1440) (as default).
[15]:
sirf = cs.SIRFModel.from_sample()
repr(sirf)
[15]:
"SIRFModel(date_range=('15Dec2025', '13Jun2026'), tau=1440, initial_dict={'Susceptible': 999000, 'Infected': 1000, 'Recovered': 0, 'Fatal': 0}, param_dict={'theta': 0.002, 'kappa': 0.005, 'rho': 0.2, 'sigma': 0.075})"
3-4. Solve ODEs
We can solve the ODEs with ODEModel().solve().
[16]:
sirf_df = sirf.solve()
cs.line_plot(sirf_df, title=f"Sample data of {sirf}", y_integer=True)
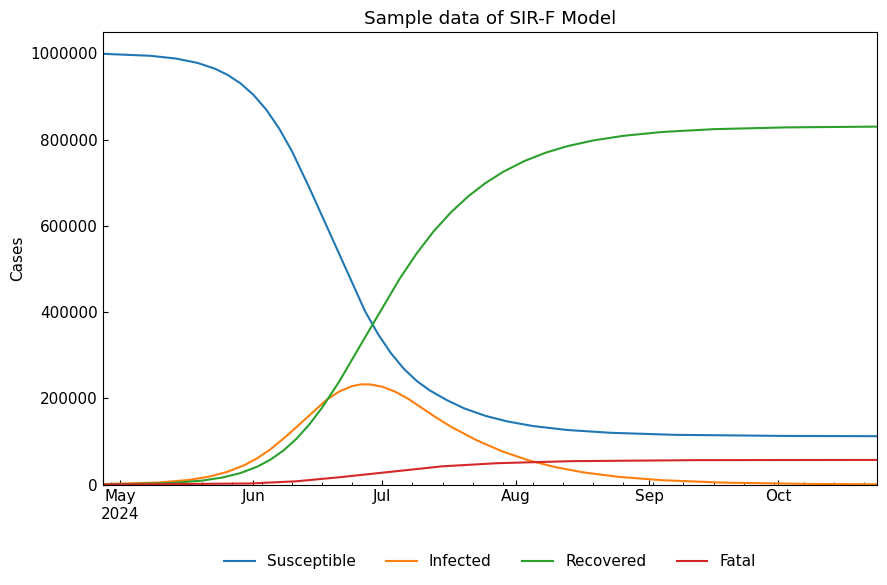
3-5. Reproduction number
Reproduction number of SIR-F model is defined as follows.
\begin{align*} R_0 = \rho (1 - \theta) (\sigma + \kappa)^{-1} = \beta (1 - \alpha_1) (\gamma + \alpha_2)^{-1} \end{align*}
[17]:
sirf.r0()
[17]:
2.5
4. SIR-F with exposed/waiting cases
4-1. Definition
\begin{align*} \mathrm{S} \overset{\beta_1 (W+I)}{\longrightarrow} \mathrm{E} \overset{\beta_2}{\longrightarrow} \mathrm{W} \overset{\beta_3}{\longrightarrow} \mathrm{S}^\ast \overset{\alpha_1}{\longrightarrow}\ & \mathrm{F} \\ \mathrm{S}^\ast \overset{1 - \alpha_1}{\longrightarrow}\ & \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\ & \mathrm{I} \overset{\alpha_2}{\longrightarrow} \mathrm{F} \\ \end{align*}
Variables:
\(\mathrm{S}\): Susceptible
\(\mathrm{E}\): Exposed and in latent period (without infectivity)
\(\mathrm{W}\): Waiting for confirmation diagnosis (with infectivity)
\(\mathrm{S}^\ast\): Confirmed and un-categorized
\(\mathrm{I}\): Confirmed and categorized as Infected
\(\mathrm{R}\): Confirmed and categorized as Recovered
\(\mathrm{F}\): Confirmed and categorized as Fatal
Parameters:
\(\alpha_1\): Direct fatality probability of \(\mathrm{S}^\ast\) (non-dimensional)
\(\alpha_2\): Mortality rate of Infected cases \(\mathrm{[1/min]}\)
\(\beta_1\): Exposure rate (the number of encounter with the virus in a minute) \(\mathrm{[1/min]}\)
\(\beta_2\): Inverse of latent period \(\mathrm{[1/min]}\)
\(\beta_3\): Inverse of waiting time for confirmation \(\mathrm{[1/min]}\)
\(\gamma\): Recovery rate \(\mathrm{[1/min]}\)
4-2. Non-dimensional SEWIR-F model
4-3. Create sample data
We use SEWIRFModel class, a child class of ODEModel. They have class method .from_sample(date_range=None, tau=1440) (as default).
[18]:
sewirf = cs.SEWIRFModel.from_sample()
repr(sewirf)
[18]:
"SEWIRFModel(date_range=('15Dec2025', '13Jun2026'), tau=1440, initial_dict={'Susceptible': 994000, 'Exposed': 3000, 'Waiting': 2000, 'Infected': 1000, 'Recovered': 0, 'Fatal': 0}, param_dict={'theta': 0.002, 'kappa': 0.005, 'rho1': 0.2, 'rho2': 0.167, 'rho3': 0.167, 'sigma': 0.075})"
3-4. Solve ODEs
We can solve the ODEs with ODEModel().solve().
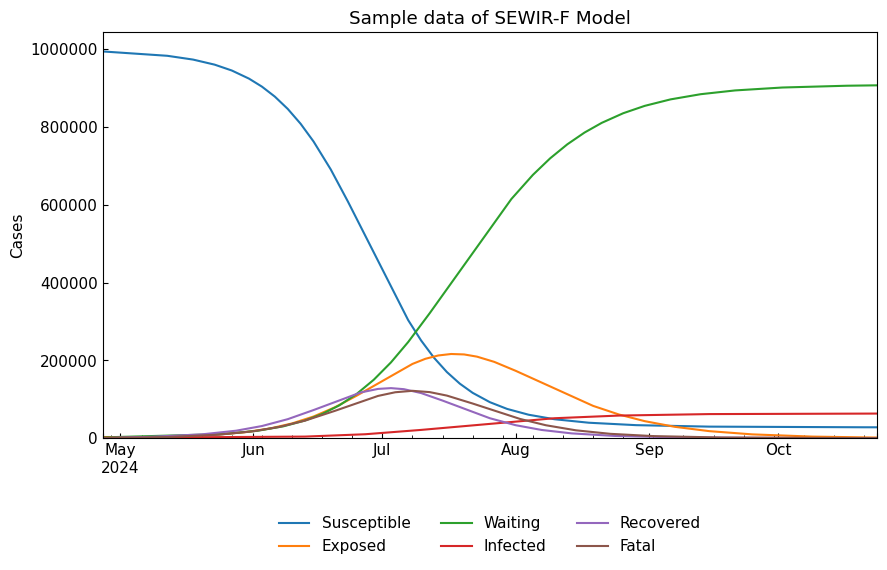
[19]:
sewirf_df = sewirf.solve()
cs.line_plot(sewirf_df, title=f"Sample data of {sewirf}", y_integer=True, bbox_to_anchor=(0.5, -0.3), ncol=3)
4-5. Reproduction number
Reproduction number of SEWIR-F model is defined as follows.
\begin{align*} R_0 = \rho_1 /\rho_2 * \rho_3 (1-\theta) (\sigma + \kappa)^{-1} \end{align*}
[20]:
sewirf.r0()
[20]:
2.49
5. SIR-F with vaccination
Vaccination is a key factor to prevent outbreak as you know.
In the previous version, we defined SIR-FV model with \(\omega\) (vaccination rate) and
However, SIR-FV model was removed because vaccinated persons may move to the other compartments, including “Susceptible”. Please use SIR-F model for simulation and parameter estimation with adjusted parameter values, considering the impact of vaccinations on infectivity, its effectivity and safety.
6. SIR-F with re-infection
Re-infection (Recovered -> Susceptible) is sometimes reported and we can consider SIR-S (SIR-FS) model. However, this is not implemented at this time because we do not have data regarding re-infection. SIR-F model could be the final model in our data-driven approach at this time.
Re-infection changes the parameter values of SIR-F model. There are two patterns.
If re-infected case are counted as new confirmed cases and removed from “Recovered” compartment, \(\sigma\) will be decreased.
If re-infected cases are counted as new confirmed cases and NOT removed from “Recovered” compartment, \(\rho\) will be increased because “Susceptible” will be decreased.
Thank you!